Here is the hook.

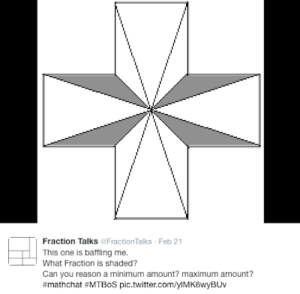
Before continuing on, try and make an estimate. What is too small? What is too big? What sections can you easily identify?
Maybe you fit into one of the following strategies (They are not mutually exclusive), or maybe you want to switch after reading them. (I know I did).

1) From @suffolkmaths

The “square” he refers to is one of the smaller 5 squares that make up the plus sign. Using this understanding of 1/5, he is able to place his entire reasoning into a single tweet. Pretty efficient if you ask me. Because each obtuse, shaded triangle has a base of the entire (smaller) square, and a height of half of a square, the area is one quarter of the square. Four groups of one quarter (actually of 1/20th of the whole) makes one entire square. Since there are five squares total, the shaded area is 1/5.

2) From @KhatriMath

In response, she classifies her strategy as more complex. At its root, they are doing the same thing–trying to mash the area into a single square representing 1/5. She also employs the area formula for a triangle. There is a moment that she uses similar triangle notation, but it doesn’t seem to play a huge role in the argument.

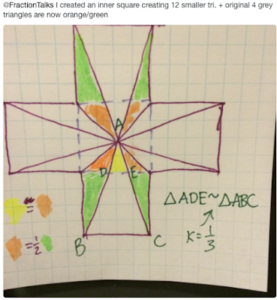
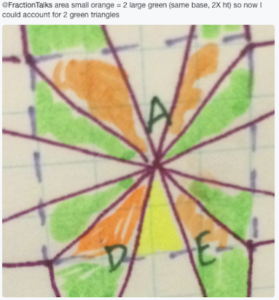
She first establishes a congruency between the yellow and orange sections. She is then left with a 2-to-1 relationship between the green and orange to complete the migration to the middle square. At the end, the middle square is easily observed as 1/5 of the whole. The strategy has a dynamic feel to it.

3) From @HRSBMathematics

This had me immediately curious. After asking for some further clarification, it was a very cool visual interpretation that still had connections to the previous two. There still was an area calculation going on,

but now there was a distinct division of the entire 3×3 grid into thirds. The idea of fifths emerges when the corners (each half shaded) are subtracted.

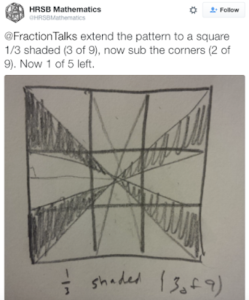
There are now 3 sets of 4 triangles that can be envisioned as rotating around the center like a pinwheel. Well, if the one entire group is shaded and there are three total groups, the shaded portion represents 1/3 of the 9 smaller squares. (Or three smaller squares total). It follows that the corners need to be subtracted to get back to the original shape. Each is half shaded, and there are four of them. So, you will subtract 2 aggregate squares of shading. If 3 squares were shaded originally, and you lost 2, you re left with one square left. Once again, the square is 1/5 of the original plus sign shape.

I love this!!

4) From @Simon_Gregg

Here, a different “base shape” is defined. Actually, two of them are used. Simon does such an elegant job of depicting them. They are given names (house and triangle), and values. He then uses subtraction to calculate the “house-but-not-triangle” area. This term warms my heart.

This sort of unique verbiage signals unique sense-making. A sort of local dialect emerges from the classroom (in this case, twitter). The shape is not dissected into triangles and squares, but sections of house-but-not-triangles. Beautiful.
_________________________________________________
It is my hope that Fraction Talks play out exactly like this. Depending on your grade level, you will get differing levels of intricacy. Honour multiplicity, entertain diversity. Allows students to use formulas, envision pinwheeling, define new terms, and play with the relationships.

Damian Watson built this Geogebra animation of how he visualizes the 1/5th. It is stunningly beautiful.

I would love to further spotlight various classroom levels of reasoning. If you have stories from your Fraction Talks, please share. I believe it is crucial that teachers see productive implementation.